镜像态的那些坑

• 表面态与镜像态
  • 表面态(Surface States, SS)
  • 镜像态(Image Potential States, IPS)
• 计算过程
  • 计算参数
    • 足够的空带
    • 足够的真空层
    • 偶极校正
  • 验证计算结果
    • PDOS 法
    • 实空间分布法
    • 能带法
• 附录
  • 镜像势表达式的推导

本文是帮实验组计算表面态与镜像态相关性质时所遇到一些坑的总结。

限于 DFT 理论上的缺陷（使用指数函数逼近库仑势，从而加速收敛）， DFT 并不能算准 IPS 的能级（误差在 \(\pm 0.3eV\)左右），但有的实验又需要从 DFT 计算获得一些关于 IPS 的信息，于是即使 DFT 不能算准，也无大碍。在这个过程中本人似乎不止一次掉入坑 中，于是把这个过程记录下来，即便对后人没什么帮助，也算是对自己学习印迹的一丝收藏 吧。

表面态与镜像态

表面态(Surface States, SS)

顾名思义，表面态就是在物体 表面 附近存在的电子态¹。表面意味着边界的存在， 边界外是真空，边界内是原子。正因为存在从体相到真空的剧烈变化，表面的原子存在不饱和键，即悬挂键。这些悬挂键由那些在体相内本应成键的电子贡献，受这些电子影响，物体的 表面 会出现一些新的、相对弥散的电子态，这些电子态被称为表面态。

镜像态(Image Potential States, IPS)

将一个电荷放在无限大的导体表面（这里假设表面是平面），导体内部会发生极化，导致内部电荷重新分布，从而产生一个静电势。这个静电势等效于导体内一个带相反电性的镜像电荷产生的静电势，因而被称为镜像势。电子因镜像势会在导体表面 外 形成一些相对弥散的态，这些态就是镜像态。

镜像势的势能曲线是反比例曲线：

\[ V(z) = - \frac{\beta e^2}{4\pi \epsilon_{0} \cdot 4z} \]

上式中 \(\beta = \displaystyle\frac{\epsilon_r-1}{\epsilon_r+1}\)

所以电子满足方程：

\[ \begin{aligned} \frac{\hbar^2}{2m_e} \nabla^2 \Psi + V(z)\Psi &={} E\Psi \newline \frac{\hbar^2}{2m_e} \nabla^2 \Psi - \frac{\beta e^2}{4\pi \epsilon_{0} \cdot 4z} \Psi &={} E\Psi \end{aligned} \]

这个方程看起来很眼熟，它十分类似于氢原子 Schrodinger 方程。由于这个电子只在 \(z\) 方向上受镜像电荷作用，因而在 \(xy\) 方向上是自由的，所以它能量可以通过求解一维氢原子 Schrodinger 方程得到：

\[ E_n = -\frac{0.85}{n^2}\frac{(\epsilon_r-1)^2}{(\epsilon_r+1)^2} \quad \text{eV} \]

其中 \(n\) 是主量子数，分子 0.85eV 正好是氢原子基态能量的 \(\dfrac{1}{4^2}\) 。 所以镜像态也可以根据主量子数的不同来区分出不同的能级。求解过程可以在一篇文章²中查到；镜像势的表达式的推导过程详见附录。

严格地说，镜像态也是表面态的一种³。一般而言，镜像态在真空能级以下 1eV 以内， DFT 算出的 IPS 能级可能会超过真空能级，但在实际上是不太可能的，即使真的有，实验上也不大能测得到。

计算过程

事实上计算出镜像态，并不需要改太多的东西。下面在介绍如何设置计算参数的同时以 Ag(111) 上吸附苯分子为例阐述如何从结果中分析是否存在 IPS 。

计算参数

这里使用的晶格是 Ag(111) 的 \(3\times3\) 表面，上表面放置了一个苯分子，结构如图：

足够的空带

如果体系比较小， VASP 默认取的 NBANDS 是足够找到 IPS 的；但当体系特别大的时候， 默认的 NBANDS 可能不太会覆盖到 IPS ，这时需要增加 NBANDS ，一般加到真空能级以上 3eV 就足够了，实际上这里只是需要 VASP 能较为 精确 地算对真空能级附近的态， 而标号接近 NBANDS 的能带不准确，表现在能带图上就是色散关系就像被生生截断了一样， 且呈锯齿状；此外，如果在实空间展开这个态会发现这个它像是随机生成的一样，没用使用价值分布。关于真空能级怎么算，详见之前的博文。

这里使用的体系里因为原子数比较适中，不用额外增加 NBANDS 。

足够的真空层

镜像态在真空层中，因此需要足够的真空层来容纳它，一般而言 30A 真空层可能还不算够。 但要注意 VASP 在算高度超过 70A 的晶格时会很难收敛。

这里使用的体系加了 50A 的真空层，已经足够放下上表面的 IPS 。

偶极校正

如果 Slab 表面没有吸附其它原子/分子，则不必对体系进行偶极校正，否则需要校正，具体过程参见之前的博文。

偶极校正效果如图：

验证计算结果

这里的「验证」与其说是验证，不如说是寻找。前面提到， IPS 是一种相对「弥散」的态， 它「弥散」的性质决定了怎么去 Identify IPS 。这里总结了几种「找」 IPS 的方法。

PDOS 法

一个态比较「弥散」说明它的局域性（locality）比较低，反映在物理图像里就是它投影在原子上的态比较少。因此我们可以在通过不同能带在原子上的投影大小来判断它是否是 IPS。

幸运地是 VASP 可以通过 LORBIT = .TRUE. 来输出 PROCAR 文件，它包含了每个能带在所有原子上的投影大小，顺便说一句， PROCAR 还包含不同角动量的投影大小。

先结构弛豫，再进行自恰计算得到 PROCAR 后，可以通过以下方法查看这个态在所有原子上的投影之和：

打开 PROCAR ，定位到真空能级 ⁴ 附近 \(\Gamma\) 点的能带

1
2
3
4
5
6
7

band    35 # energy    3.23957699 # occ.  0.00000000

ion      s     py     pz     px    dxy    dyz    dz2    dxz  x2-y2    tot
    1  0.002  0.000  0.000  0.000  0.000  0.000  0.002  0.000  0.000  0.004
    2  0.001  0.000  0.001  0.000  0.000  0.000  0.000  0.000  0.000  0.002
    ......
tot    0.005  0.000  0.004  0.000  0.000  0.000  0.004  0.000  0.000  0.013

看最后一行 tot 0.005 ... ，最右边也有一个 tot ，两者交叉的的值 0.013 即为这条能带在整个系统上的投影大小，换言之，局域度的大小。那么这个值越小则它是 IPS 的可能性越高。比如上面的能带 PDOS 中整体的 PDOS 之和只有 0.013 ，说明它的局域度很小，那么这个态非常弥散，有可能是 IPS 。

实空间分布法

仅仅是通过能带的 PDOS 还不足以确认这条带是不是 IPS ，有些费米能级附近的带总体 PDOS 也很小，但不是 IPS 。这时就需要其它方法来看了，比如本节要介绍的实空间分布法。

IPS 在实空间的分布特征相当明显：

1. 它们在表面以外，并且随着主量子数的升高有着对应个数的波包；
2. 每个波包对应的空间分布呈明显的近自由电子态的特征。

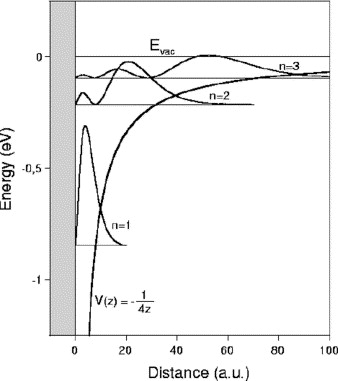
如下图⁵所示：

上面图中 \(n=1\) 的 IPS 只有一个波包， \(n=2\) 时有两个波包， \(n=3\) 时有三个， 以此类推下去……

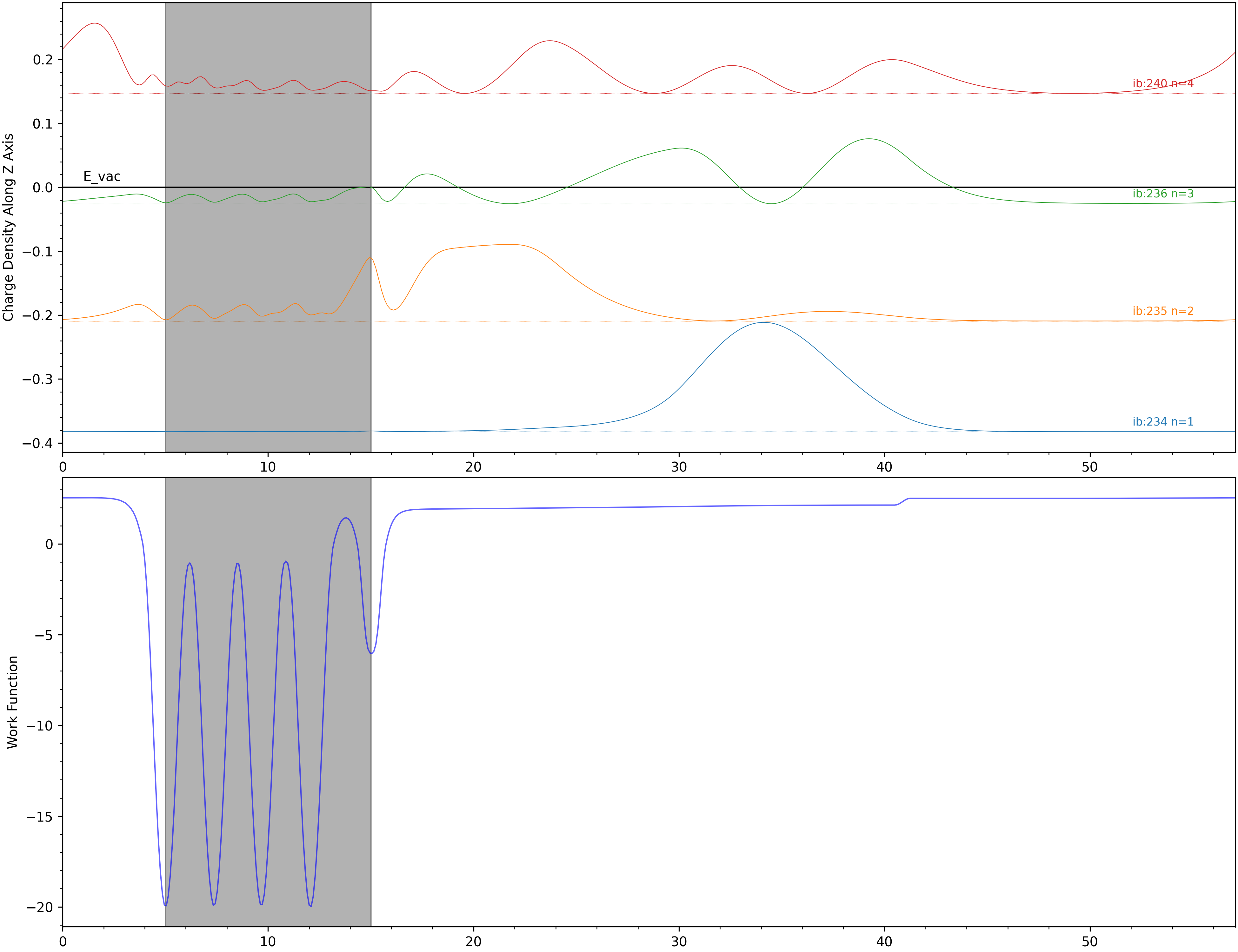
对于第一个特征，我们可以对波函数的模平方作 \(z\) 方向上的分布，数出表面外有多少个峰，注意区分 Slab 的上表面和下表面，只有上表面的波包应该被计入在内。

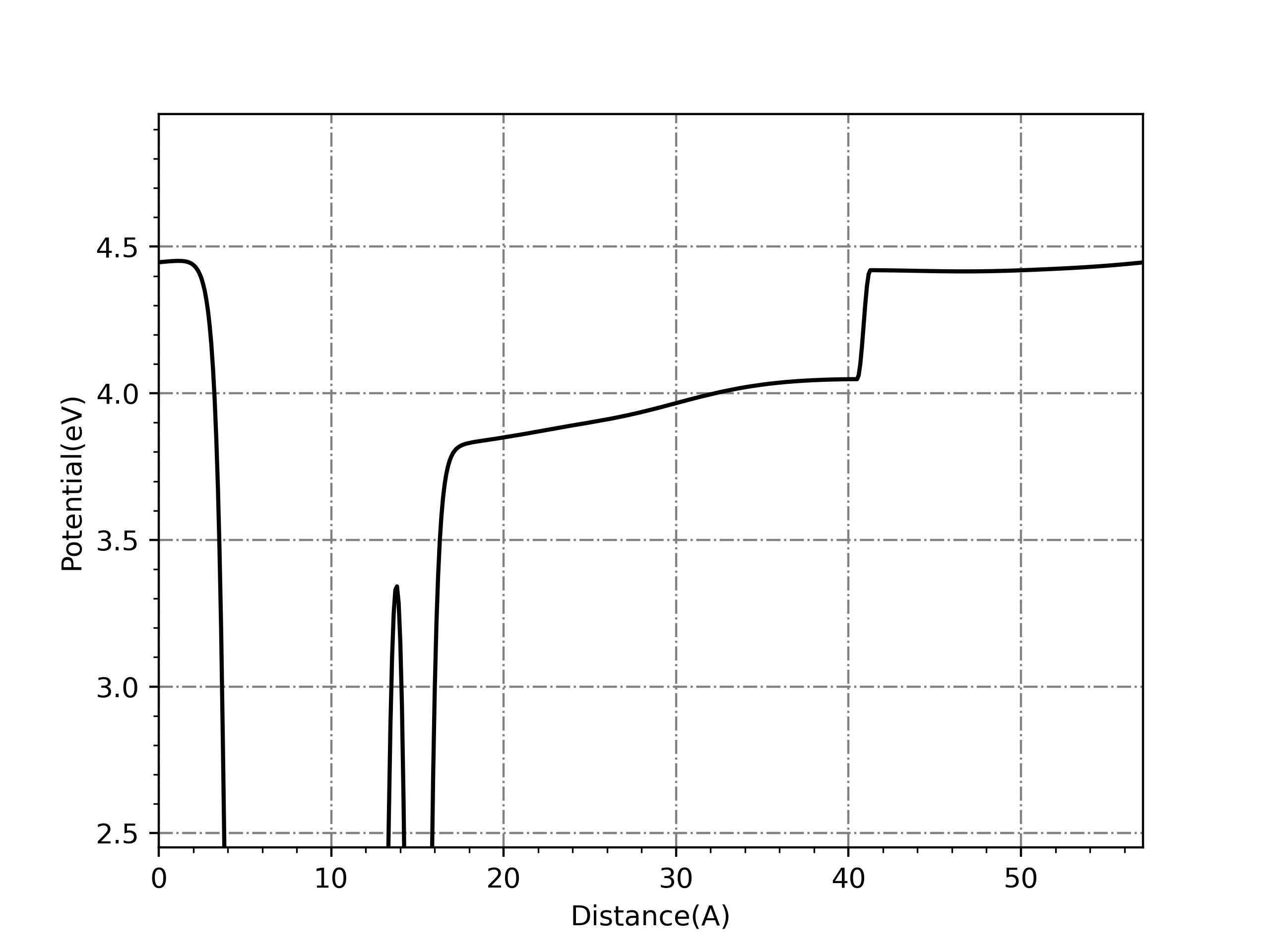
在 Benzene on Ag(111) 体系中，对应的 IPS 实空间分布曲线如下：

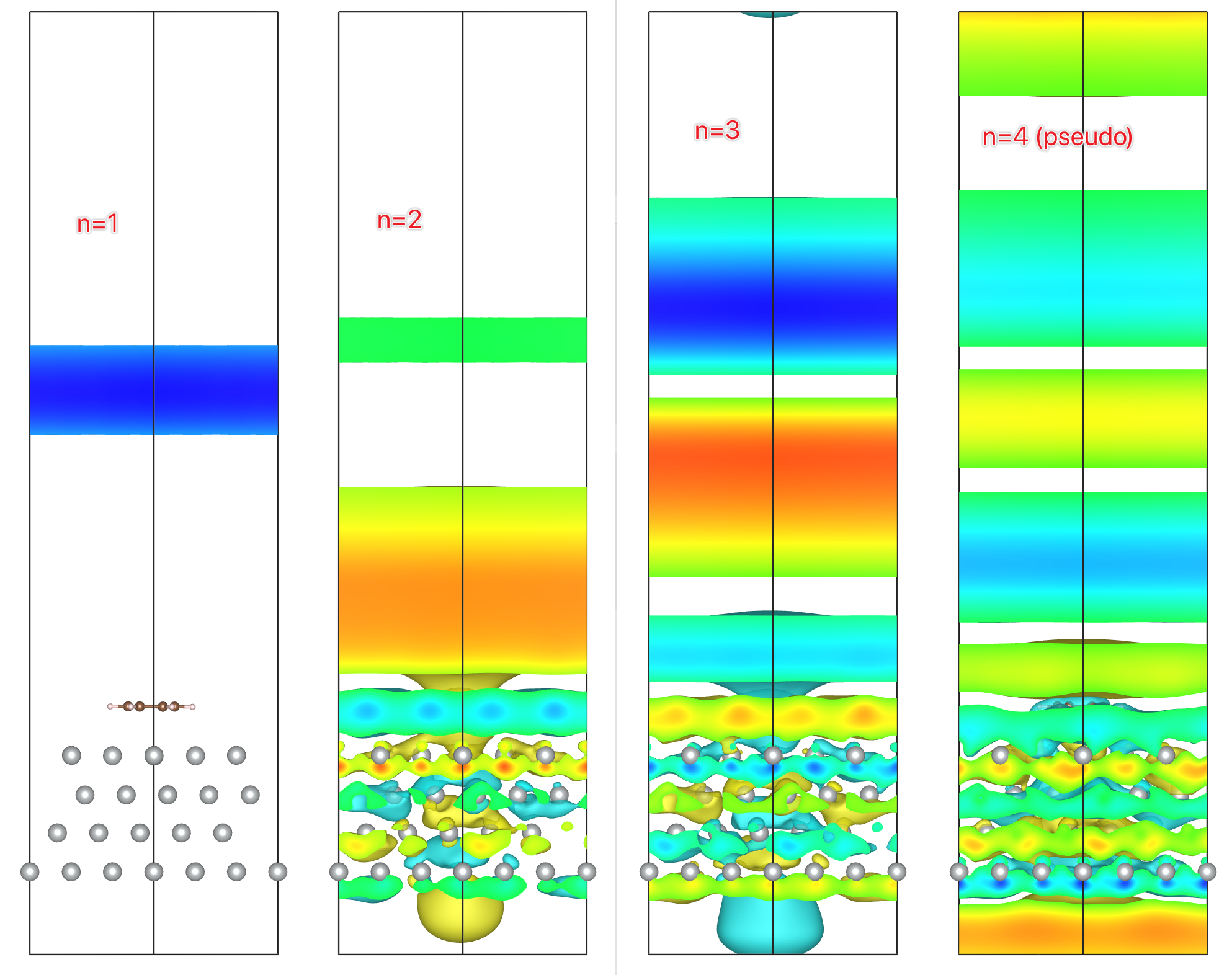
如果只看 \(z\) 方向上的波函数觉得不放心，可以把某条带在实空间的分布画出来，如果它在真空中，并且上下表面近似为平面，即在水平方向上为近自由电子，也就可认为它是 IPS ，如下图所示：

实际上，图上所标 \(n=4\) 的曲线并不真的是 IPS ，它的能量在真空能级以上，并且它的能量也不符合 \(\dfrac{1}{n^2}\) 的规律。如果仔细验证的话， \(n=1,2,3\) 的能量也并不符合这个规律，这就是 DFT 理论的局限所致，想要再算得更准，需要更大的代价。

能带法

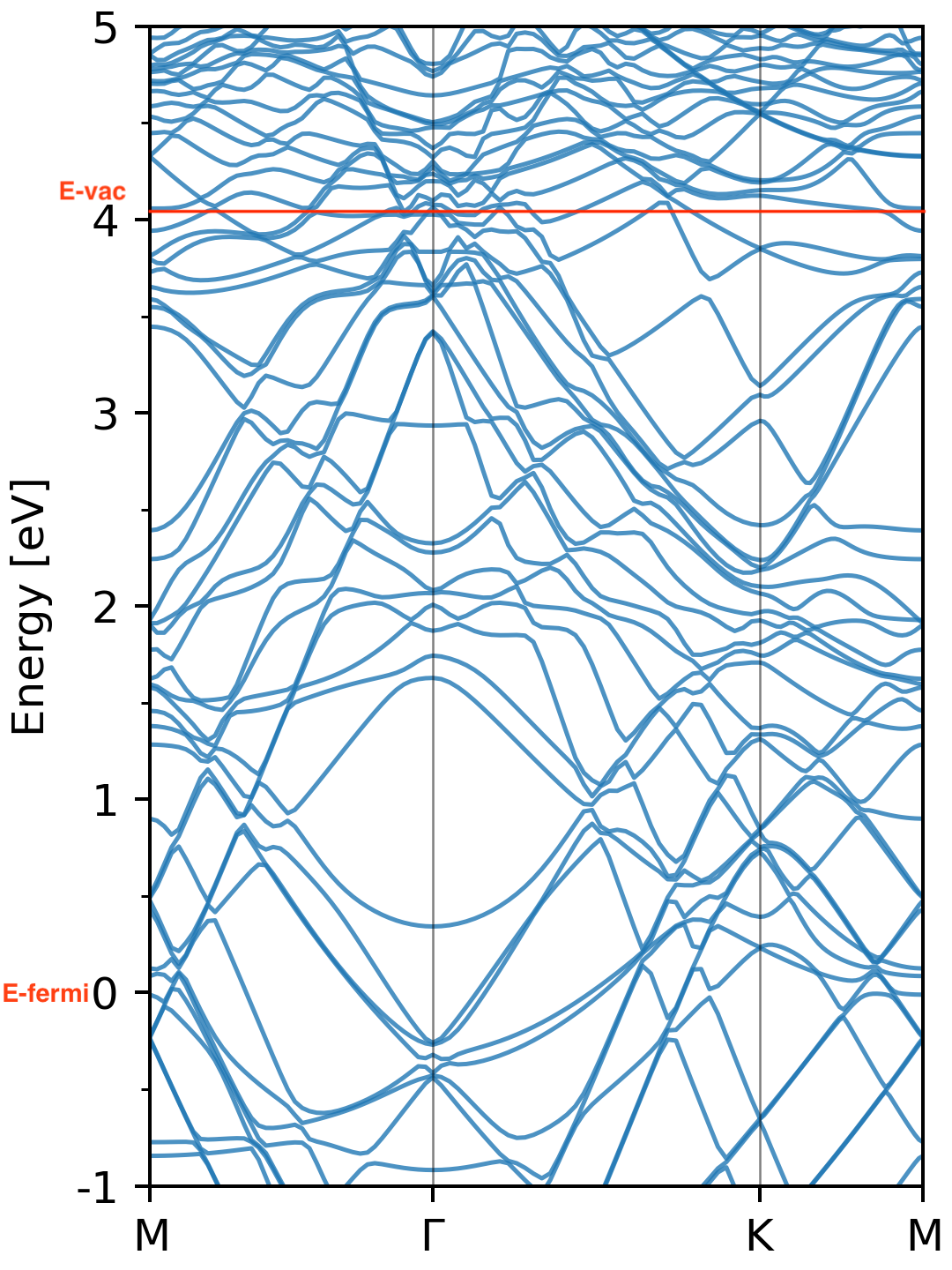
以上是在单点能静态计算的基础上进行的分析，如果已经画出了这个体系的能带图，从能带图上可以更加清晰地反映出 IPS 的特征。

能带图的横坐标量纲是动量，纵坐标是能量。一个自由电子的能量全部由动能贡献，因此它的能量与动量的关系就是

\[ E = E_k = \frac{p^2}{2m} = \frac{g^2}{2m_e} \]

\(E\) 与 \(g\) 呈二次函数式色散关系，那么只要某个带的色散关系与抛物线相似，就有理由认为某能带可能是 IPS ，比如下面的图中 4 eV 附近 \(\Gamma\) 点的能带明显呈抛物线色散关系，而它们也确实算是 IPS 。

如果更有耐心的话，可以算一下那几条带的相对有效质量，如果接近 1 ，就可以很明确地说明这几条带是 IPS ，可惜本人不太想再算这个（实际就是懒），这个就算作「读者自证不难」吧2333。

附录

镜像势表达式的推导

这里更一般地推导一下两种介质界面处镜像势的表达式，过程参考自⁶。

假设有两种介质 1 和 2，它们的介电常数分别为 \(\epsilon_1\) 和 \(\epsilon_2\) ，有电荷 \(q\) 在介质 1 中，如下图所示：

现在将问题分成两部分来看：分别计算介质 1 和介质 2 中电场强度。

在介质 1 中任取一点 \(P\) ，同时认为 \(q\) 的镜像电荷等效带电量为 \(q'\) ，则 \(P\) 点的受力如下图所示

此处的电场强度为

\[\begin{aligned} V_1 &={} \frac{1}{4\pi \epsilon_1} \left( \frac{q}{R_1} + \frac{q'}{R_2} \right) \newline R_1 &={} \sqrt{(z-d)^2 + r^2} \newline R_2 &={} \sqrt{(z+d)^2 + r^2} \newline E_z &={} -\frac{\partial V_1}{\partial z} = \frac{1}{4\pi\epsilon_1} \left[ \frac{q(z-d)}{R_1^3} + \frac{q'(z-d)}{R_2^3} \right] \newline E_r &={} -\frac{\partial V_1}{\partial r} = \frac{1}{4\pi\epsilon_1} \left[ \frac{qr}{R_1^3} + \frac{q' r}{R_2^3} \right] \newline \end{aligned}\]

现在考虑介质 2 中的电场强度，由于经过一个介面，介电常数分布发生了改变，所以在介质 2 中所感受到的原来电荷的等效电荷为 \(q''\) 。

P 点的电场强度可以计算出来：

\[\begin{aligned} V_2 &={} \frac{1}{4\pi\epsilon_2} \frac{q''}{R_3} \newline R_3 &={} \sqrt{(z-d)^2 + r^2} \newline E_z^{(2)} &={} -\frac{\partial V_2}{\partial z} = \frac{1}{4\pi\epsilon_2} \frac{q'' (z-d)}{R_3^3} \newline E_r^{(2)} &={} -\frac{\partial V_2}{\partial r} = \frac{1}{4\pi\epsilon_2} \frac{q'' r}{R_3^3} \newline \end{aligned}\]

在界面处应用导体介质界面上的边界条件：

\[\begin{cases} z = 0 \implies R_1 = R_2 = R_3 = R \newline D_z^{(1)} = D_z^{(2)} \newline E_r^{(1)} = E_r^{(2)} \newline \end{cases}\]

即：

\[\begin{aligned} \epsilon_1 E_z^{(1)} & = {} \epsilon_2 E_z^{(2)} \newline \implies \epsilon_1 \frac{1}{4\pi\epsilon_1} \frac{(q-q')d}{R^3} & = {} \epsilon_2 \frac{1}{4\pi\epsilon_2} \frac{q'' d}{R^3} \newline \implies q - q' &={} q'' \end{aligned}\]

\[\begin{aligned} E_r^{(1)} &={} E_r^{(2)} \newline \implies \frac{1}{4\pi\epsilon_1} \frac{(q+q')r}{R^3} &={} \frac{1}{4\pi\epsilon_2} \frac{q'' r}{R^2} \newline \implies \frac{q+q'}{\epsilon_1} &={} \frac{q''}{\epsilon_2} \end{aligned}\]

联立上面两式，可以得到

\[ q' = -\frac{\epsilon_2 - \epsilon_1}{\epsilon_2 + \epsilon_1} q \]

如果用相对介电常数 \(\epsilon_r = \dfrac{\epsilon_2}{\epsilon_1}\) ，上面式子还能简化为

\[ q' = -\frac{\epsilon_r - 1}{\epsilon_r + 1} q = -\beta q \]

这就是前文中镜像电荷表达式中 \(\beta\) 的来源。可以看出，如果 \(\epsilon_r < 1\) ，镜像电荷的符号与原来电荷相同。

电荷 \(q\) 的受力以及势能表达式：

\[\begin{aligned} F(z) &={} -\frac{\beta q^2}{4\pi \epsilon_0 (2z)^2} \quad \beta = \frac{\epsilon_r-1}{\epsilon_r+1} \newline V(z) &={} -\frac{\beta q^2}{4\pi \epsilon_r \cdot 4z} \end{aligned}\]

文中第一节的表达式得证。