使用数值方法求解单电子 Schrodinger 方程

单粒子定态 Schrodinger 方程
有限差分法
有限元法
- 定态 Schrodinger 方程的变分弱解形式
- 程序实现及结果验证
总结及吐槽
- 吐槽

经常有人觉得会解薛定谔方程会给人一种很厉害的感觉（尤其是对还没学过 QM QC 等课程中学生小朋友而言），确实，现在能写出解析解的 Schrodinger 方程屈指可数；而且仅仅增加粒子数量不考虑各种修正就足以使求解的难度上升一大截。不过在这里我们不考虑多个粒子的情况，也不考虑什么相对论效应 blabla ，我们只考虑一个电子在一个任意势场下的定态 Schrodinger 方程，然后来用数值方法求解这个方程，得到电子的波函数并可视化，顺便验证一下教材上各种电子轨道的分布图，体验一把亲手解 Schrodinger 方程的感觉。

这里本文是在实空间的笛卡尔坐标系进行求解。

单粒子定态 Schrodinger 方程

考虑一个电子在势场 \(V\) 中，它的定态 Schrodinger 方程是

\begin{equation} \hat{H} \Psi(x, y, z) = E\Psi(x, y, z) \end{equation}

如果这个势场是 \(V = 0\) ，并且限定这个电子在一个边长为 \(a\) 的箱子内，此时 Schrodinger 方程就变成了

\begin{equation} -\frac{\hbar^2}{2m} \left( \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2} \right) \Psi(x, y, z) = E\Psi(x, y, z) \end{equation}

这个方程可以写出解析解¹ （参加过考试的同学应该能默写这个公式了）：

\[E = (n_x^2 + n_y^2 + n_z^2) \frac{h^2}{8ma^2}\]

\[ \begin{aligned} \Psi(x, y, z) &={} X(x)Y(y)Z(z) \newline &={} \sqrt{\frac{8}{a^3}}\sin(\frac{n_x \pi x}{a})\sin(\frac{n_y \pi y}{a})\sin(\frac{n_z \pi z}{a}) \end{aligned} \]

这是三维情况下的解，如果体系只有一维，它的能级表达式是

\[ E = \frac{n^2 h^2}{8ma^2} \newline \Psi(x) = \sqrt{\frac{2}{a}} \sin(\frac{n \pi x}{a}) \]

这是它们的解析解，也是我们后面验证结果正确性的参考。以上结果的推导请参考任意一本《量子力学》或《量子化学》或者《结构化学》。

有限差分法

所谓有限差分法，就是有限差分来近似导数，从而寻求微分方程近似解的方法。针对导数的有限差分操作可以参考 Wikipedia ²，简单来说就是用各种近似方法来逼近导数的值。

假设存在一个离散的函数 \(f(x), x = x_1, x_2, … , x_n\) ，并且 \(x_{i+1} - x_{i} = \Delta x\) 为一定值，根据有限差分的推导，可以得到下面的结论：

一阶导数的离散化

这里使用一种最为常见的离散化方法来近似一阶导数：

\begin{equation} f'(x_i) \approx \frac{f(x_i+\Delta x) - f(x_i - \Delta x)}{2\Delta x} = \frac{f(x_{i+1}) - f(x_{i-1})}{2\Delta x} \end{equation}

再假设 \(f(x)\) 可以写成一个列向量 \(\ket{f} = \begin{bmatrix} f(x_1), f(x_2), \cdots, f(x_n) \end{bmatrix}^T\) ，那么一阶导数算符 \(\dfrac{d}{dx}\) 可以写成

\[\frac{d}{dx} \begin{bmatrix} f(x_1)\newline f(x_2) \newline \vdots \newline f(x_n) \end{bmatrix} = \frac{1}{2\Delta x} \begin{bmatrix} 0 & 1 & & & \newline -1 & 0 & 1 & & \newline & -1 & 0 & \ddots & \newline & & \ddots & \ddots & 1 \newline & & & -1 & 0 \end{bmatrix} \cdot \begin{bmatrix} f(x_1)\newline f(x_2) \newline \vdots \newline f(x_n) \end{bmatrix} \]

这是在没有处理边界条件的情况下的一阶导数算符，如果考虑周期性边界条件，上式矩阵的左下角和右上角分别为 1 和 -1 。此外这种方法近似得到的一阶导的精度是 \(O((\Delta x)^2)\) ，更高阶的近似及其它非对称的方法请参考本节之前提到的 Wikipedia 。

二阶导数的离散化

比较常见的二阶导数离散化方法如下：

\begin{equation}\begin{aligned} f'(x_i+\frac{1}{2} \Delta x) &\approx{} \frac{f(x_i + \Delta x) - f(x_i)}{\Delta x} = \frac{f(x_{i+1}) - f(x_i)}{\Delta x} \newline f'(x_i-\frac{1}{2} \Delta x) &\approx{} \frac{f(x_i) - f(x_i - \Delta x)}{\Delta x} = \frac{f(x_i) - f(x_{i-1})}{\Delta x} \newline f''(x_i) &\approx{} \frac{ f'(x_i+\frac{1}{2} \Delta x) - f'(x_i-\frac{1}{2} \Delta x) }{\Delta x} \newline &={} \frac{ f(x_{i+1}) + f(x_{i-1}) - 2f(x_i) }{(\Delta x)^2} \end{aligned}\end{equation}

同样，它也可以用矩阵的形式表达出来：

\[ \frac{d^2}{dx^2} \begin{bmatrix} f(x_1)\newline f(x_2) \newline \vdots \newline f(x_n) \end{bmatrix} = \frac{1}{(\Delta x)^2} \begin{bmatrix} -2 & 1 & & & \newline 1 & -2 & 1 & & \newline & 1 & -2 & \ddots & \newline & & \ddots & \ddots & 1 \newline & & & 1 & -2 \end{bmatrix} \cdot \begin{bmatrix} f(x_1)\newline f(x_2) \newline \vdots \newline f(x_n) \end{bmatrix} \]

如果需要考虑周期性边界条件，矩阵的左下角和右上角都应为 1 。这种方法近似的精度是 \(O((\Delta x)^2)\) 。

一维系统 Hamiltonian 的构造及求解

一维势箱模型系统的求解

Hamiltonian 的整体表达式为

\[ H = T + V \]

如果系统只有一维，那么 Hamiltonian 很好构造，直接在 \(T\) 的基础上加上势能即可

\[H = \frac{1}{(\Delta x)^2} \begin{bmatrix} -2 & 1 & & & \newline 1 & -2 & 1 & & \newline & 1 & -2 & \ddots & \newline & & \ddots & \ddots & 1 \newline & & & 1 & -2 \end{bmatrix} + \begin{bmatrix} V_1 & & & \newline & V_2 & & \newline & & \ddots & \newline & & & V_n \end{bmatrix} \]

然后我们的问题就变成了

\[ H \ket{\psi} = E\ket{\psi} \]

这是一个典型的本征值问题，只要对 \(H\) 进行对角化就可以得到我们想到的能量 \(E\) 和波函数 \(\ket{\psi}\) 。下面是它的程序实现（本文使用 Julia 作为有限差分法的实现语言）

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57


#!/usr/bin/env julia

using LinearAlgebra;
using SparseArrays;
using Arpack;
using Plots;

################################################################################
#
#                           Constants Part
#
################################################################################

const N = 5000;                 # sample points
const len = 1.0;                # box length

const k = 3.8099821161548593;   # hbar^2 / (2*m_e) = (Å^2) / eV
const m = 1.0;                  # relative mass of electron

const nev = 4;                  # number of eigen values to be covered

x = LinRange(0.0, len, N);
const dx = len / N;

################################################################################
#
#                           Hamiltonian Part
#
################################################################################

T_ = sparse(-2.0I, N, N);
T_[diagind(T_,  1)] .= 1.0;
T_[diagind(T_, -1)] .= 1.0;
T_ *= -k / (m * dx * dx);

T = deepcopy(T_);
H = T;

println("Hamiltonian constructed, start solving ...");
@time λ, ϕ = eigs(H, nev=nev, which=:LM, sigma=0.0);
@show λ

################################################################################
#
#                           Hamiltonian Part
#
################################################################################

for i in 1:nev
    ϕ[:,i] ./= norm(ϕ[:, i]) * sqrt(dx)   # Normalization
    @assert sum(ϕ[:, i].^2) * dx ≈ 1.0    # verify the norm: ∫ |ϕ|² dx == 1
end

@show maximum(ϕ[:, 1])

p = plot(x, ϕ, layout=(2, 2), size=(800, 600));
savefig(p, "./1D-particle-in-a-box-eigvec.svg");

1
2
3
4


Hamiltonian ready, start solving ...
  1.991257 seconds (7.25 M allocations: 439.625 MiB, 8.56% gc time, 99.53% compilation time)
λ = [37.58797833051402, 150.3518984879221, 338.29171597315013, 601.4073566198176]
maximum(ϕ[:, 1]) = 1.4140720924720651

下面我们来验证一下程序的结果：

程序中有 \(k = \hbar^2 / 2m_e = 3.80998 (\mathrm{Å^2/eV})\) ，它把一些物理常数打包处理并化为原子单位制，因此在和解析解对比时也要以此为准，此外程序中定义 \(a=1Å\) ，没有显式处理边界条件。势箱模型中解析解为

\[ E = \frac{n^2 h^2}{8ma^2} = \frac{\hbar^2}{2m} \cdot \frac{4\pi^2 n^2}{4a^2} = \frac{kn^2\pi^2}{a^2} \]

代入 \(k\) 和 \(a\) ，得到 \(E_1 = 37.6029953761\) ，与数值解 \(\lambda_1=37.58797833051402\) 对比相当接近，继续验证 \(\lambda_2\) 、 \(\lambda_3\) 等可以发现它们也符合 \(n^2\) 的增长曲线（读者可自行验证）。

再来验证一下波函数：

它显然符合正弦曲线的特征，并且在边界处为 0 ，最大值为 1.414072 与归一化因子 \(\sqrt{2} = 1.414213\) 相差也在允许范围内，因此现在可以放心地说，如果 \(T\) 没有特殊边界条件处理，它的边界条件就是使边界处的波函数为 0 ，这在后面的计算中可以得到进一步验证。

带有 Chulkov 势的一维势箱系统求解

上面的系统中电子不受束缚， Hamiltonian 里没有势能这一项，这也就没有验证势能项加在对角线上的合理性，下面我们使用一种于二十年前被提出的势能函数来验证这一点。

Chulkov ³ 等于 1997 年提出一种势能用于模拟出金属表面的镜像态。它以金属表面为 0 点， 0 以下使用正弦函数模拟金属的体相内的势能， 0 及以上使用正弦及指数函数等模拟金属表面以外的镜像势，它有如下形式：

\[ V_m(z) = \begin{cases} -A_{10} + A_1 \cos \left( \frac{2\pi}{d_m} z \right) & z \le 0 \newline -A_{20} + A_2 \cos(\beta z) & 0 < z \le z_1 \newline -A_3 \exp\left[-\alpha(z-z_1)\right] & z_1 < z \le z_\mathrm{im} \newline \dfrac{\exp\left[ -\lambda (z-z_\mathrm{im}) \right]-1}{4(z-z_\mathrm{im})} & z > z_\mathrm{im} \end{cases} \]

体现在图像上是这个样子的：

这里选择用于 Ag(111) 表面的各参数，代码如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93


#!/usr/bin/env julia

# Reference: Image potential states on metal surfaces: binding energies and wave functions
#             https://www.sciencedirect.com/science/article/pii/S0039602899006688

using LinearAlgebra;
using SparseArrays;
using Arpack;
using Plots;


const N = 15000;
const len = 150.0;

const k = 3.8099821161548593    # hbar^2 / (2*m_e) /(Å^2) / eV
const k_c = 14.39964547842567   # (e*e / (4 * np.pi * epsilon_0))  # measured in eV / Å
const m = 1.0                   # mass of electron

const dx = len / N;

const nev = 8;

################################################################################
#
#                                Potential Part
#
################################################################################

#=
#
# V1(z) = -A10 + A1*cos(2pi*z/dm)    z <= 0
# V2(z) = -A20 + A2*cos(beta*z)      0 < z <= z1
# V3(z) = -A3 * exp(-alpha*(z-z1))   z1 < z <= zim
# V4(z) = (exp(-lambda*(z-zim))-1.0) / (4.0*(z-zim))  z > zim
#
=#

const a0 = 0.529;# A, bohr raidus
const as = 4.43; # a.u.
const A10 = 9.64;# eV
const A1 = 4.30; # eV
const A2 = 3.8442; # eV
const beta0 = 2.5649; # 1/a.u.
const zim0 = 2.35; # a.u.

const dm = as * a0; # A
const A20 = A10 + A2 - A1; # eV
const beta = beta0 / a0; # A^-1
const zim = zim0 * a0; # A
# const A3 = A2 / sqrt(2); # eV
const z1 = 5*pi/(4*beta); # A
const A3 = A20 - A2*cos(beta*z1); # eV
const alpha = - A2*beta*sin(beta * z1) / A3; # A^-1
const lambda = 4*A3*exp(-alpha*(zim - z1)) / k_c; # A^-1

@show A10 A1 dm A20 A2 beta A3 alpha z1 lambda zim

z = LinRange(-len/2, len/2, N);
V = similar(z);

@. V[z<=0]      = -A10 + A1 * cos(2pi * z[z<=0] / dm)
@. V[0<z<=z1]   = -A20 + A2 * cos(beta * z[0<z<=z1])
@. V[z1<z<=zim] = - A3 * exp(-alpha * (z[z1<z<=zim] - z1))
@. V[z>zim]     = (exp(-lambda * (z[z>zim] - zim)) - 1.0) / (4.0 * (z[z>zim] - zim)) * k_c

################################################################################
#
#                           Hamiltonian Part
#
################################################################################

Ident = sparse(1.0I, N, N);
T_ = sparse(-2.0I, N, N);
T_[diagind(T_,  1)] .= 1.0;
T_[diagind(T_, -1)] .= 1.0;
T_ *= -k / (m * dx * dx);

T = deepcopy(T_);

H = T;
H[diagind(H)] .+= V;
Vmin = -1.0;

λ, ϕ = eigs(H, nev=nev, which=:LM, sigma=min(0, Vmin));
@show λ

for i in 1:nev
    ϕ[:,i] ./= norm(ϕ[:,i]) * sqrt(dx)      # normalization
    @assert  sum(ϕ[:,i].^2) * dx ≈ 1.0      # test norm
end

p = plot(z, ϕ.^2, layout=(4,2), size=(800, 600));
savefig(p, "./1D-chulkov-eigvec.svg");

下面是计算结果与文献值对比

λ	计算结果(eV)	文献值(eV)	实验值(eV)
1	-0.788	−0.77	-0.77
2	-0.674	-	-
3	-0.533	-	-
4	-0.330	-	-
5	-0.208	-0.22	-0.23
6	-0.103	-0.095	-0.10
7	-0.061	-0.053	-0.052
8	-0.031	-	-

上面表中有一些态主要分布在体相内，文献和实验中没有测到。为更明显地对比镜像态与 bulk 态的区别，这里使用 \(|\phi|^2\) 作图：

显然， \(\phi_2\) 、 \(\phi_3\) 和 \(\phi_4\) 大部分都处于体相内，从包络线的形状看，它们类似于刚刚讨论过的势箱内的态，但这些态不属于镜像态，所以在与实验对比时应排除在外。而 \(\phi_1\) 、 \(\phi_5\) 、 \(\phi_6\) 和 \(\phi_7\) 在真空中的部分存在波包，且波包的数量刚好对应主量子数 \(n\) ，如 \(\phi_5\) 在 \(x\ge 0\) 的部分有两个波包，它就是 \(n=2\) 对应的本征态。

二维及更高维系统的 Hamiltonian 构造与求解

一维情况下我们可以直接使用二阶导而无需其它处理即可构造出动能算符，但在更高维度下要如何构造动能算符，以及 Hamiltonian 呢？

高维 Laplacian 的离散化

根据 Wikipedia ⁴ 上关于离散 Laplacian （拉普拉斯算符）的描述，多维离散 Laplacian 是一维离散 Laplacian 的 Kronecker Sum （克罗内克和）。

例如对于一个二维系统：

\[ L = \bold{D}_\bold{xx} \oplus \bold{D}_\bold{yy} = \bold{D}_\bold{xx} \otimes \bold{I} + \bold{I} \otimes \bold{D}_\bold{yy} \]

其中 \(\bold{D}_\bold{xx}\) 、 \(\bold{D}_\bold{yy}\) 表示在 \(x\) 、 \(y\) 方向上的 Laplacian 矩阵， \(\bold{I}\) 是单位矩阵。

注意，上式中 “\(\oplus\)” 表示 Kronecker Sum 操作而不表示矩阵 Direct Sum （直和）操作，尽管它们所用的符号是一样的；而 “\(\otimes\)” 则可以理解为 Kronecker Product 或者 Direct Product （直积）操作，因为在此处可以认为两种操作等价。

相应地，对于一个三维系统，它的 Laplacian 应该是

\[ L = \bold{D}_\bold{xx} \otimes \bold{I} \otimes \bold{I} + \bold{I} \otimes \bold{D}_\bold{yy} \otimes \bold{I} + \bold{I} \otimes \bold{I} \otimes \bold{D}_\bold{zz} \]

下面通过计算二维势箱内的电子能级来验证上面式子的正确性。

假设二维势箱是边长 \(a = 1 \rm{Å}\) 的正方形，其中的电子满足 Schrodinger 方程：

\[\begin{aligned} -\frac{\hbar^2}{2m_e}(\frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2}) \psi = E\psi \end{aligned}\]

它的 Hamiltonian 只包含 Laplacian ，解析解为

\[\begin{aligned} E &={} (n_x^2 + n_y^2)\frac{h^2}{8ma^2} \newline \psi(x, y) &={} \frac{2}{a}\sin(\frac{n_x \pi x}{a}) \sin(\frac{n_y \pi y}{a}) \end{aligned}\]

程序实现如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74


#!/usr/bin/env julia

using LinearAlgebra;
using SparseArrays;
using Arpack;
using Plots;

################################################################################
#
#                           Constants Part
#
################################################################################

const N = 200;                 # sample points
const len = 1.0;                # box length

const k = 3.8099821161548593;   # hbar^2 / (2*m_e) = (Å^2) / eV
const m = 1.0;                  # relative mass of electron

const nev = 8;                  # number of eigen values to be covered

x = LinRange(0.0, len, N);
y = LinRange(0.0, len, N);
const dx = len / N;
const dy = len / N;

################################################################################
#
#                           Hamiltonian Part
#
################################################################################

Tx = sparse(-2.0I, N, N);
Tx[diagind(Tx,  1)] .= 1.0;
Tx[diagind(Tx, -1)] .= 1.0;
Tx *= -k / (m * dx * dx);
Ix = sparse(1.0I, N, N);

Ty = sparse(-2.0I, N, N);
Ty[diagind(Ty,  1)] .= 1.0;
Ty[diagind(Ty, -1)] .= 1.0;
Ty *= -k / (m * dx * dx);
Iy = sparse(1.0I, N, N);

T_ = kron(Tx, Iy) + kron(Ix, Ty);

T = deepcopy(T_);
H = T;

println("Hamiltonian constructed, start solving ...");
@time λ, ϕ = eigs(H, nev=nev, which=:LM, sigma=0.0);
@show λ

################################################################################
#
#                           Visualization Part
#
################################################################################

for i in 1:nev
    ϕ[:,i] ./= norm(ϕ[:, i]) * dx   # Normalization
    @assert sum(ϕ[:, i].^2) * dx^2 ≈ 1.0    # verify the norm: ∫ |ϕ|² dx == 1
end

@show maximum(ϕ[:, 1])

ψ = reshape(ϕ, N, N, nev);

p1 = surface(x, y, ψ[:, :, 1], title="ψ_1");
p2 = surface(x, y, ψ[:, :, 2], title="ψ_2");
p3 = surface(x, y, ψ[:, :, 3], title="ψ_3");
p4 = surface(x, y, ψ[:, :, 4], title="ψ_4");
p = plot(p1, p2, p3, p4, layout=(2, 2), size=(800, 500));
savefig(p, "./2D-particle-in-a-box-eigvec.svg");

解得本征值与解析解对比如下：

\(\lambda\)	\(n_x^2 + n_y^2\)	\(E_{\rm numerical}\) (eV)	\(E_{\rm analytical}\) (eV)
1	1 + 1 = 2	74.458	75.206
2	4 + 1 = 5	186.136	187.961
3	1 + 4 = 5	186.136	187.961
4	4 + 4 = 8	297.814	300.737
5	9 + 1 = 10	372.236	375.922
6	1 + 9 = 10	372.236	375.922
7	9 + 4 = 13	483.914	488.698
8	4 + 9 = 13	483.914	488.698

解得的本征值相差还是不小的，但总体趋势是一致的。解得波函数如下（限于篇幅原因只列举前四个）:

根据波函数形状判断，它们与量子数的对应关系如下：

\(\psi\)	\(n_x\)	\(n_y\)	\(E\) (eV)
1	1	1	74.458
2	2	1	186.136
3	1	2	186.136
4	2	2	297.814

在归一化波函数后，求得振幅为 1.990 ，与 \(\dfrac{2}{a} = 2\) 相差无几。

由此可见，使用 Kronecker Sum 构造的 Laplacian 解出的结果是正确的。

高维 Hamiltonian 的构造与求解

已经有了高维的 Laplacian ，我们需要把势能项和 Laplacian 组合起来得到 Hamiltonian 。显然，我们需要把势能加到对角项上，但要注意一个问题，就是 Laplacian 的对角项与格点的对应关系：

\[ L = \bold{D}_\bold{xx} \otimes \bold{I} \otimes \bold{I} + \bold{I} \otimes \bold{D}_\bold{yy} \otimes \bold{I} + \bold{I} \otimes \bold{I} \otimes \bold{D}_\bold{zz} \]

我们不妨令 \(\bold{D}_\bold{xx}\) 为 \(\bold{X}\) ， \(\bold{D}_\bold{yy}\) 为 \(\bold{Y}\) ， \(\bold{D}_\bold{zz}\) 为 \(\bold{Z}\)，根据 Kronecker Product 的运算过程（详见 Wiki），最后得到的矩阵对角线应该是

\[\begin{bmatrix} \bold{X}_{11} \bold{Y}_{11} \bold{Z}_{11} & & & \newline & \bold{X}_{11} \bold{Y}_{11} \bold{Z}_{22} & & \newline & & \bold{X}_{11} \bold{Y}_{11} \bold{Z}_{33} & \newline & & & & \ddots \end{bmatrix}\]

上式中 \(\bold{Z}\) 的对角线，即最后一个维度的下标增长得最快；对应地，在加和势能项时，也应该是最后一个维度增长最快，这恰好是访问一个行主序的多维数组元素时的访问顺序。也就是说我们只需要按照行主序的顺序把多维的势能数组展开为一维数组，然后加和到 Laplacian 上即可得到 Hamiltonain ：

\[H = T + \begin{bmatrix} V_{111} & & & \newline & V_{112} & & \newline & & V_{113} & \newline & & & \ddots \end{bmatrix}\]

此处我们选取静态氢原子的电子为求解对象，它的 Shrodinger 方程是这个形式

\[ -\frac{\hbar^2}{2m_e} \nabla^2 \psi - \frac{e^2}{4\pi \epsilon_0} \frac{1}{r} \psi = E\psi \]

下面是程序实现，注意 Julia 的数组是列主序，因此在组合 Hamiltonian 时需要转换；除此之外受计算机性能和辣鸡 ARPACK 的限制，这里每个维度只取 50 个点，每个维度各取 30Å 的长度。

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101


#!/usr/bin/env julia

using LinearAlgebra;
using SparseArrays;
using Arpack;
using WriteVTK;

# Auxiliary function
function mgrid(xs...)
    it = Iterators.product(xs...);
    ret = [];
    for i in 1:length(xs)
        push!(ret, getindex.(it, i));
    end
    return ret;
end


################################################################################
#
#                                Constants Part
#
################################################################################

const k   = 3.8099821161548593  # hbar^2 / (2*m_e) /(Å^2) / eV
const k_c = 14.39964547842567   # (e*e / (4 * np.pi * epsilon_0))  # measured in eV / Å
const m   = 1.0                 # mass of electron

const xlen = 30.0;
const ylen = xlen;
const zlen = xlen;

const N = 50;
const dx = xlen / N;

# generate the grid
const x = range(-xlen/2, xlen/2, length=N);
const y = range(-ylen/2, ylen/2, length=N);
const z = range(-zlen/2, zlen/2, length=N);

const nev = 10;

################################################################################
#
#                                Potential Part
#
################################################################################

gx, gy, gz = mgrid(x, y, z);
function potential(gx, gy, gz) ::AbstractArray
    r = sqrt.(gx.^2 + gy.^2 + gz.^2);
    r[r .< 0.0001] .= 0.0001;
    return -k_c ./ r;
end

V = potential(gx, gy, gz);
Vmin = minimum(V)


################################################################################
#
#                                Hamiltonian Part
#
################################################################################

# Kinetic part
Identity = sparse(1.0I, N, N);

T_ = sparse(-2.0I, N, N);
T_[diagind(T_,  1)] .= 1.0;
T_[diagind(T_, -1)] .= 1.0;

T_ .*= -k / (m * dx*dx)

T = kron(T_, kron(Identity, Identity)) +
    kron(Identity, kron(T_, Identity)) +
    kron(Identity, kron(Identity, T_));

# Hamiltonian
H = deepcopy(T);
H[diagind(H)] .+= permutedims(V, [3, 2, 1])[:];


# Solve the equation Hψ = Eψ
@time λ, ϕ = eigs(H, nev=nev, which=:LM, sigma=min(0, Vmin));
@show λ


################################################################################
#
#                                Visualization Part
#
################################################################################

vtk_grid("HydrogenAtom", x, y, z) do vtk
    for i in 1:nev
        ϕ[:, i] ./= norm(ϕ[:,i]) * dx * sqrt(dx);
        @assert sum(ϕ[:,i].^2) * dx^3 ≈ 1.0
        vtk["phi_$i"] = reshape(ϕ[:, i], N, N, N);
    end
end

结果与解析值对比

\(\lambda\)	\(n\)	\(E_{\rm numernical}\) (eV)	\(E_{\rm analytical}\) (eV)
1	1	-10.713	-13.6
2	2	-3.417	-3.4
3	2	-3.417	-3.4
4	2	-3.417	-3.4
5	2	-3.031	-3.4
6	3	-1.515	-1.51
7	3	-1.515	-1.51
8	3	-1.515	-1.51
9	3	-1.474	-1.51
10	3	-1.474	-1.51

本征值与解析值对应得并不好，尤其是基态的能量，与解析解相差了近 3eV ，这是因为 \(1s\) 态主要局域在原子核附近，而求数值解时每个维度只取了 50 个点，

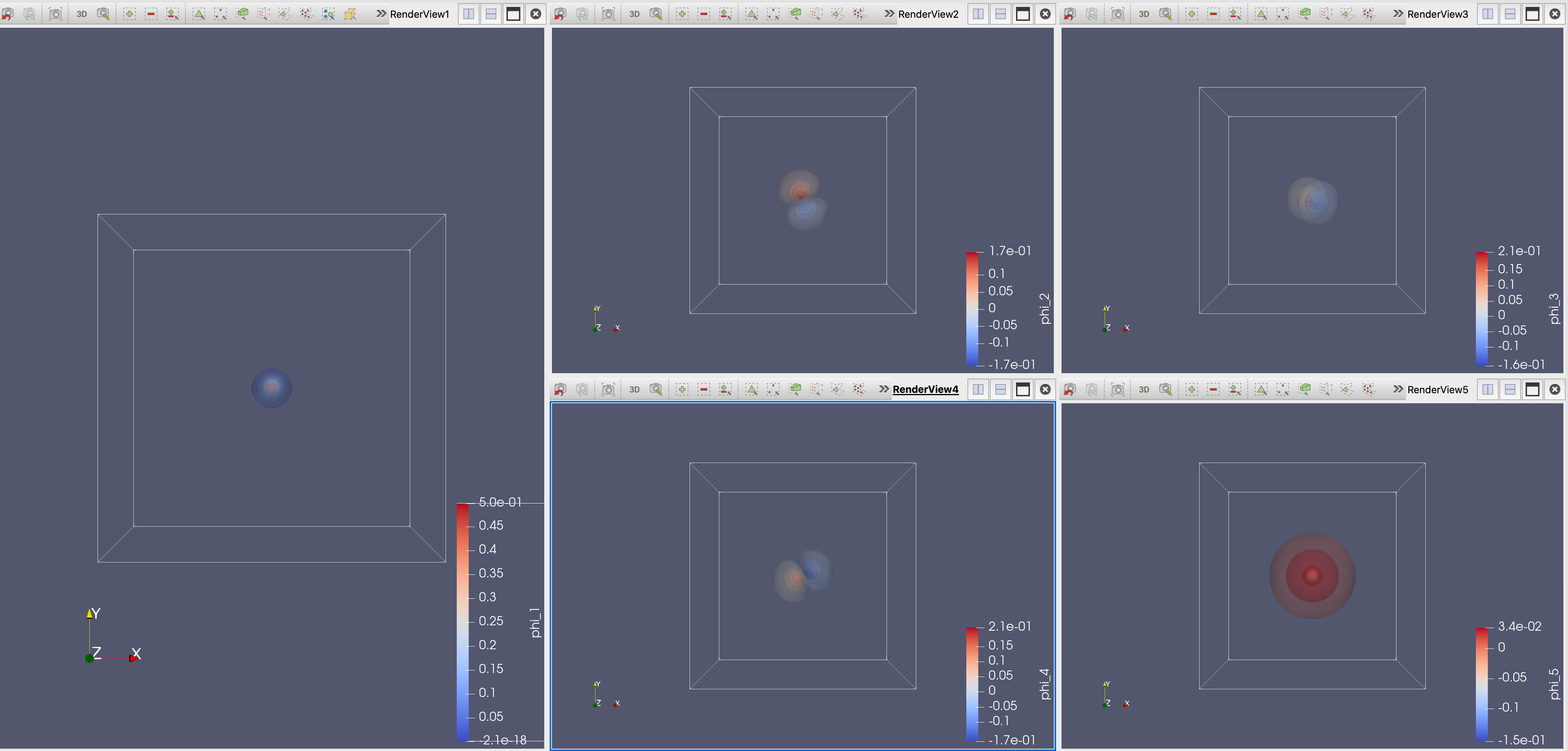
本征态如下（这里只取前五个态）：

它们分别对应氢原子的 \(1s\) 态、 \(2p_y\) 态、 \(2p_z\) 态、 \(2p_x\) 态和 \(2s\) 态，抛去过于粗糙的格点和不太准的本征值不谈，它们的形状与实验上符合得还是很好的。

以上结果可以证明 Hamiltonian 的构造是合理的。

有限元法

注：本人刚刚接触 FEM ，这里只是简单谈谈有限元法，以能通过改示例跑通自己的问题为标准，因此对它的各项论述十分粗浅且可能存在错误，欢迎专业人士指正。

上面我们讨论了使用有限差分法求解 Schrodinger 方程的过程，除了有限差分法，还有一种在 CAE 领域应用非常广泛的方法——有限元法，也能用来求解 Schrodinger 方程。简单且不负责任地说，有限元与有限差分最大的区别在于有限元的元素是大小、形状均可变，并且它可以随意调整求解空间的形状以及网格的形状、局部疏密等等，这使得它可以对各种奇怪的体系进行求解。

定态 Schrodinger 方程的变分弱解形式

之前本文给出过定态 Schrodinger 方程

\[ -\frac{\hbar^2}{2m}\nabla^2 \psi + V\psi = E\psi \]

它其实是偏微分方程的 Strong Form （强解形式），而在 FEM 领域中常常使用 Weak Form （弱解形式）来描述一个偏微分方程。经过查阅资料，我找到的 Shrodinger 方程的弱解形式如下：

\[\begin{aligned} \frac{\hbar^2}{2m} \int_{\Omega} \left( \frac{\partial u}{\partial x} \frac{\partial v}{\partial x} + \frac{\partial u}{\partial y} \frac{\partial v}{\partial y} + \frac{\partial u}{\partial z} \frac{\partial v}{\partial z} \right) + \int_{\Omega} Vuv = \int_{\Omega} Euv \end{aligned}\]

上式中 \(u\) 是我们要求解的波函数， \(v\) 是测试函数， \(\Omega\) 是有限元空间。看起来这个式子和 Schrodinger 方程的强解形式差不多，只是动能项前面没有负号了。具体推导过程详见 Weak formulation of Poisson’s equation ⁵ 或 Weak formulation of quantum harmonic oscillator ⁶。

程序实现及结果验证

有了弱解形式的 Schrodinger Equation 后就可以开始使用有限元法求解了，这里使用 FreeFEM++ ⁷ 作为实现语言。

使用 FreeFEM++ 求解本征值问题时主要有以下步骤：

定义网格；
定义有限元空间；
定义需要解决的问题，即用代码表达弱解形式的偏微分方程；
调用求解器求解；
输出结果以及可视化结果等。

这里以求解氢原子为例，求解空间为 30Åx30Åx30Å 的正方体，边缘格点数为 40x40x40 ，使用 P1 有限元空间。下面是代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44


load "msh3"
load "iovtk"

int nn = 40;

real ka = 3.8099821161548593; // hbar^2 / 2m_e
real kc = 14.39964547842567; // e^2 / (4pi epsilon_0)

mesh3 Th = cube(nn, nn, nn, [30*x-15, 30*y-15, 30*z-15]);
plot(Th, wait=1);

fespace Vh(Th, P1);

cout << "Th :  nv = " << Th.nv << " nt = " << Th.nt << endl;

real sigma = -13;

macro Grad(u) [dx(u), dy(u), dz(u)] // EOM
varf a(u1, u2) = int3d(Th) (
    Grad(u1)' * Grad(u2) * ka
    - 1.0 / sqrt(x^2 + y^2 + z^2)  * u1 * u2 * kc
    - sigma * u1 * u2
    )
    //+ on(1, 2, 3, 4, 5, 6, u1=0.0)   // boundary condition
    ;

varf b([u1], [u2]) = int3d(Th) ( u1 * u2 ) ;

matrix A = a(Vh, Vh);
matrix B = b(Vh, Vh);

int nev = 20;
real[int] ev(nev);
Vh[int] eV(nev);

int k = EigenValue(A, B, sym=true, sigma=sigma, value=ev, vector=eV, tol=1e-10);

k = min(k, nev);

for (int i=0; i<k; ++i) {
    cout << " ---- " << i << " " << ev[i] << " == " << endl;
    plot(eV[i], cmm="#" + i + " EigenValue=" + ev[i], wait=true);
    savevtk("Eigen_" + i + ".vtk", Th, eV[i], dataname="EigenValue=" + ev[i]);
}

求得本征值如下：

\(\lambda\)	\(E_{\rm numerical}\) (eV)	\(E_{\rm analytical}\) (eV)
1	-10.390	-13.6
2	-3.163	-3.4
3	-3.163	-3.4
4	-2.980	-3.4
5	-2.776	-3.4
6	-1.475	-1.5
8	-1.475	-1.5
7	-1.444	-1.5
9	-1.444	-1.5
10	-1.423	-1.5

可见在这个格点密度下它的精度还是不太高，有些态甚至还比不上有限差分法的精度。

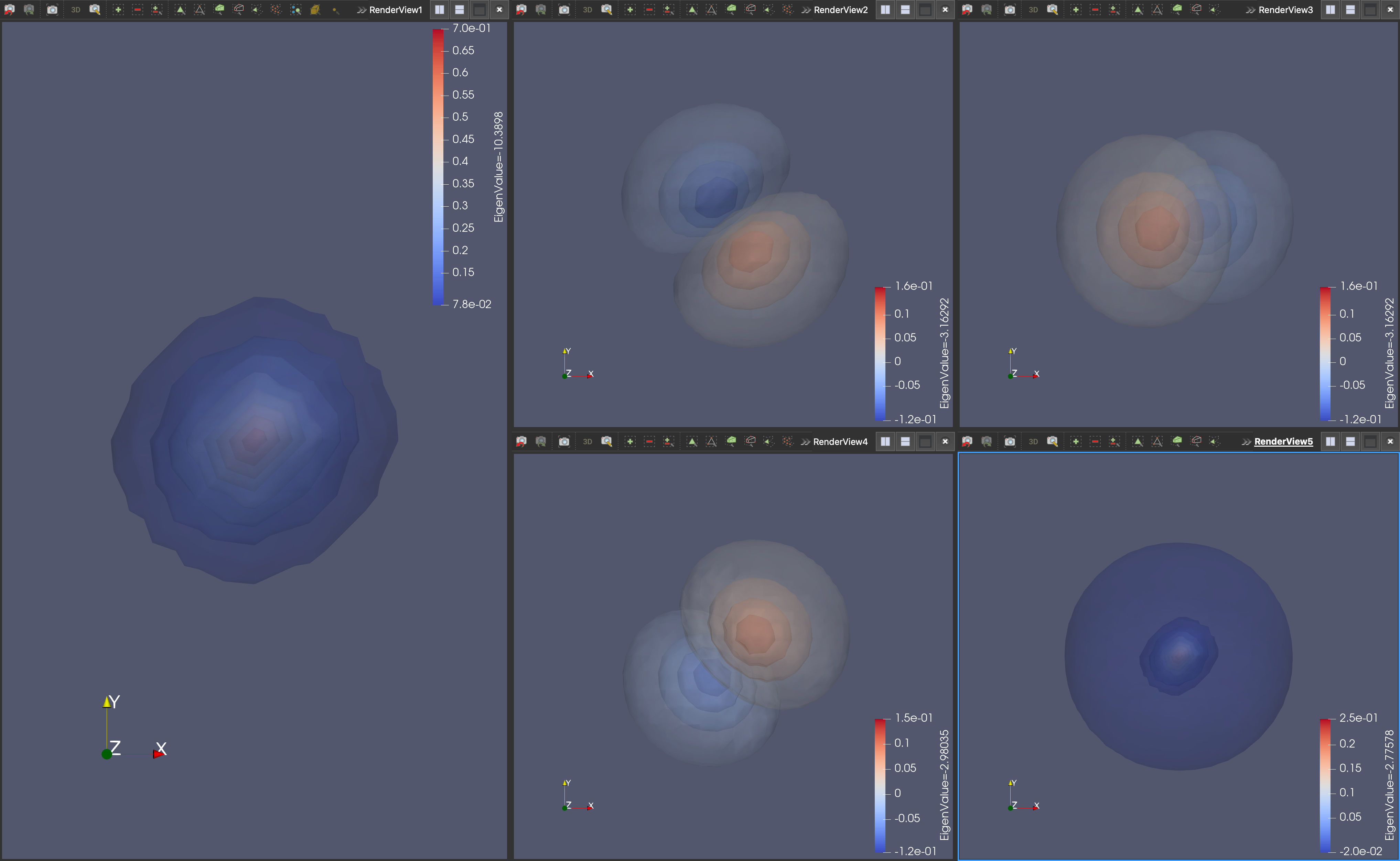
它们的本征态如下：

和有限差分法相比，它的本征态似乎更粗糙一些，实际上这是由于取的网格不够密，以及势能项 \(1/r\) 在 0 处存在奇点难以近似导致的。

尽管有这样的缺陷，但它胜在是一个成熟的开源软件，比之前随便写的 toy 要正式许多，而且它还能使用其它设计软件来建模定义求解的空间，甚至读取其它软件生成的网格进行后续的计算，最重要的一点，它可以集成并行的本征值求解器 SLEPc ⁸ 。经过测试，求解一个 150x150x75 的网格时，在 32 核的服务器上可以用 18 分钟跑完，效率还是令人满意的。

总结及吐槽

总之，本文使用了两种不同的方法在实空间直接求解单电子的 Schrodinger 方程，总体的结果还算满意。有限差分法的算法学习自 GithHub 的一个项目 qmsolve ⁹，作者甚至还把我拉到了这个项目的 Discord 讨论群（现在已经开放）继续讨论。

吐槽

有限差分法的 Hamiltonian 矩阵大小随维度的升高而急剧升高，如果一个问题能在较低的维度解决，不要使用更高的维度，通常情况后者解不动：一维问题的 Hamiltonian 大小是 \(O(N^2)\) ，而三维问题的 Hamiltonian 大小是 \(O(N^6)\) ~~，如果后面有空的话我会考虑写一下柱坐标系内 Schrodinger 方程的求解~~ 。
在使用有限差分法时格点越密，求解所需的时间越多，且耗时呈指数级增长。为此我花了将近一周多的时间在寻找 Julia 能用的并行本征值求解器上，最后发现没有能满足要求的，有几个 C++ / Python 能用的并行求解器，如 SLEPc 和 Trilinos ，但我没去尝试；
Arpack 在处理 60x60x60 的格点时就已经有点力不从心了，超算上显示它只能通过调用 BLAS 来实现部分的并行操作，且最多只有 6 个线程在跑，而且 Arpack 也确实很久没有更新了；
scipy.sparse.eigsh 的效率还不如 Julia 里的 Arpack.eigs ，前者算 50x50x50 的体系就算不动了，而且似乎在超算上用并行也没什么加速效果，尽管所有核都是满载；
FreeFEM++ 的语言乍一看挺像 C++ ，但其实区别还是相当大的，令人惊喜的是它的文档还有一个中文翻译版；
在服务器上编译 FreeFEM++ 也花了我不少时间，这个东西的 Makefile 写得让人头疼： configure 文件直接就是一个 Python 脚本，而且层层套娃，想改什么参数都不好找，那两天被弄得脑壳疼；
FreeFEM++ 支持并行操作，用更密的 Mesh 可以重复出文献上的结果；更重要的是它可以更灵活地指定边界条件；
在可视化 FreeFEM++ 的输出，即 vtk 文件时也遇到了不少麻烦，因为之前从没接触过 vtk 文件，只是听说 ParaView¹⁰ 效果最好，于是从头开始学 ParaView 。不得不说，入门时还是看视频学最快，找谷歌翻论坛很可能不知所云；
实验组最后还要求用求得的波函数计算一下位置算符的期望值，于是我又不得不去翻 ParaView 的手册找怎么操作数据。这个软件和 Python 以及 VTK 深度集成，里面自带一个 Python 解释器，但没有提供内置对象的文档，导致你面对一个 Script 框时连输入是啥都不知道，此外它的一些数据结构在原版 VTK 内还没有，那就只能靠 dir(obj) 来看它的方法列表了，通过不断地翻论坛（2018 年以前的论坛还是在邮件列表上），还是在一个人的回答中找到了相关的信息，算是顺利解决了问题，不得不说这个过程还是挺恶心人的。

这些东西可能读起来几分钟就读完了，但从接到相关的任务，到给出令实验组满意的结果，再到写出这篇博文，整整用掉了一个多月的时间，这期间试了尝试过很多次，不管是有限差分还是有限元，写过很多测试的代码但结果不正确，身边又没有可以请教人时，内心还是有一点绝望的（尤其在 6 月下半旬还夹着报账那个事），中途想过放弃，想着不如直接找个力学系的同学抛给他用 COMSOL 解出来，但最后还是通过翻论坛，厚着脸皮问 developer 等手段把想要的结果算出来了，此时觉得前面的努力还是没有白费，就是对当初对实验组的老师打包票说几天就能算出来，但实际花了近一个月这一点还是有点惭愧的。

文章目录